
A*算法
A_算法与Dijkstra算法的框架是完全一样的,**A_算法就是有启发性的Dijkstra算法**
代价函数:g(n) 表示的是从开始节点到当前n节点的代价累加
启发函数:h(n) 表示当前节点到目标节点估计所花的代价
优先级队列:维护的是 代价函数+启发函数的 节点从小到大排序 f(n)=g(n)+h(n)
每次弹出的节点就是最小的f(n)值的节点。
A*算法伪代码
维护一个优先级队列,存储所有被扩展的节点,且节点按f()值的大小自动按从小到大排列。
-所以节点的启发值h(n)是为被定义的,是不知道的,到具体的节点再计算
-优先级队列首先为空,以起始节点Xs进行初始化
-起始节点g(Xs)=0,并且初始化其它节点的代价为无穷大
-循环:
1、如果队列是空的,返回false,跳出循环
2、**弹出优先级队列中f(n)最小的节点n** [唯一与djikstra不同的地方]
3、标记节点n为被扩展节点
4、如果节点n为目标节点,返回true,跳出循环
5、找到n节点周围可以扩展的所以节点(没被扩展过)m
6、进行判断 如果g(m)为无穷大(说明其它节点也没发现过m),
7、则计算 真正的g(m)=g(n)+Cnm,然后将m节点加入到优先级队列中
8、进行判断 如果g(m)不为无穷大,有值了(说明其它节点发现过m,m已经在优先级队列中)
9、再次进行判断 如果之前发现m时计算的g(m)比g(n)+Cnm大的话
10、更新g(m)=g(n)+Cnm。
11、重复循环至步骤1
-结束循环
A* 算法步骤示例
下面是一个A_算法的演示图,每个边有个预先设置的代价g,每个节点有提前估计好的启发f
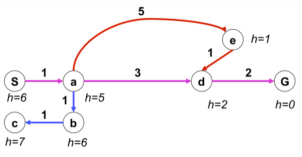
以这个图将A_ 算法运行的步骤进行一个示例:
1、首先初始化队列,将起始节点放入优先级队列中
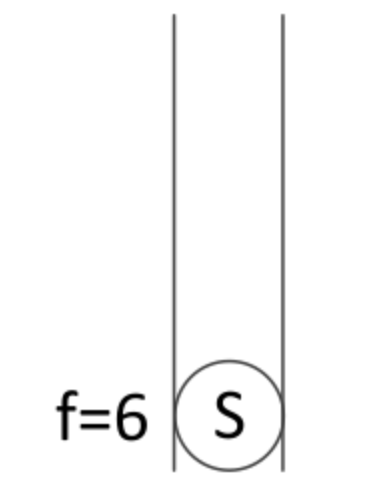
2、弹出起始节点
可扩展的节点仅有a节点,计算f(a)=g(a)+h(a)=1+5=6
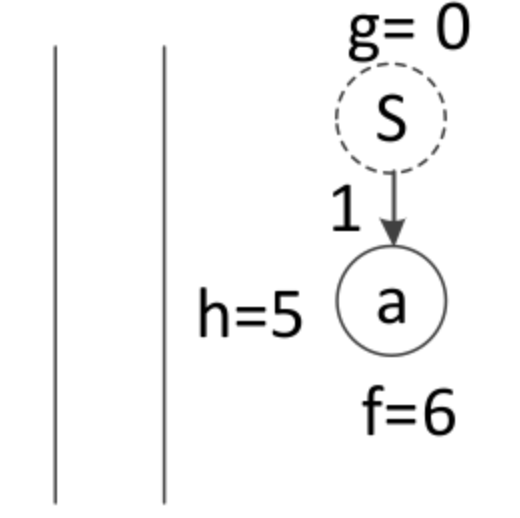
3、将扩展的节点放入优先级队列
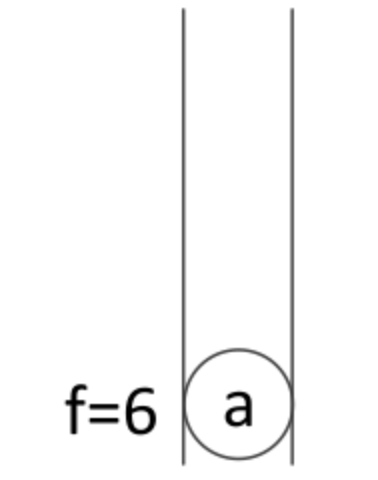
4、弹出f最小节点,扩展周围节点
弹出a节点,a节点周围可以扩展的节点为 b\d\e 。并且根据g与h值计算f值
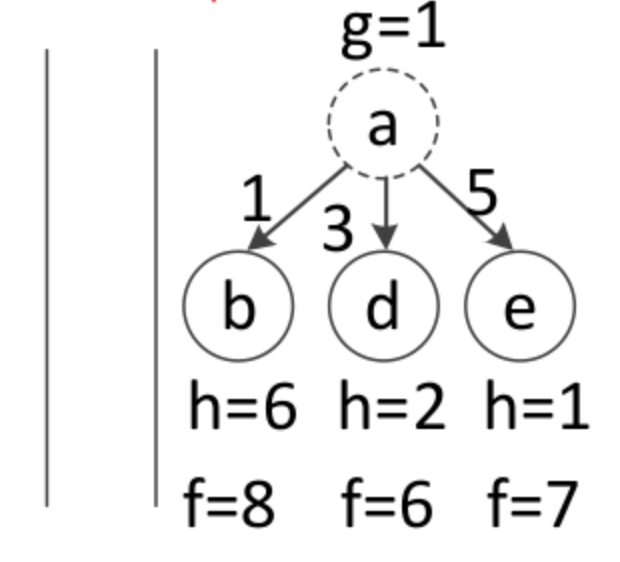
5、根据f值大小,压入队列中
d节点的f(d)=6最小,它在最下方。
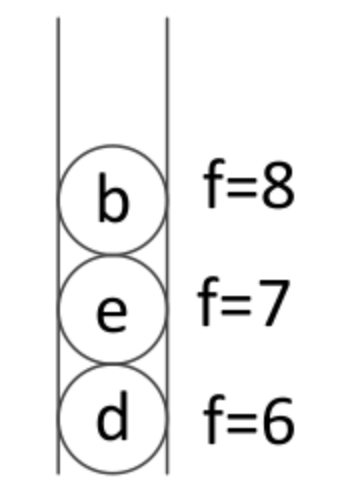
6、弹出f值最小节点 ,扩展周围节点
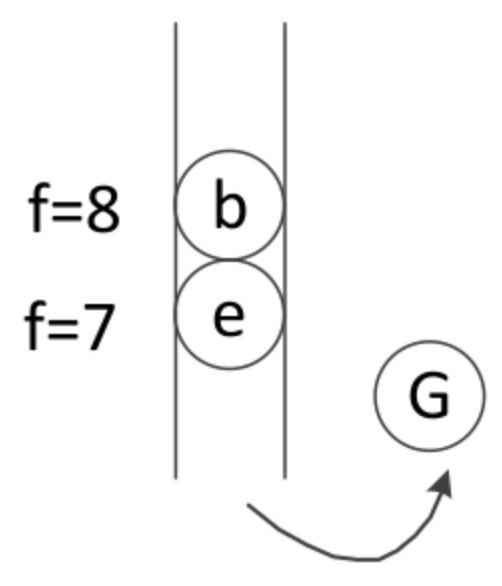
弹出d节点,可扩展节点为G节点,计算f(G)=6
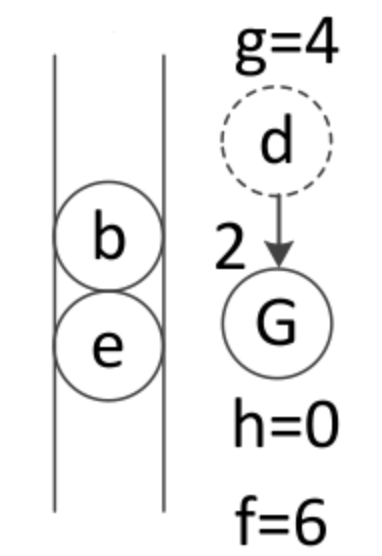
7、将最新扩展的节点加入优先级队列中,并进行排序
G最小,排到最底下
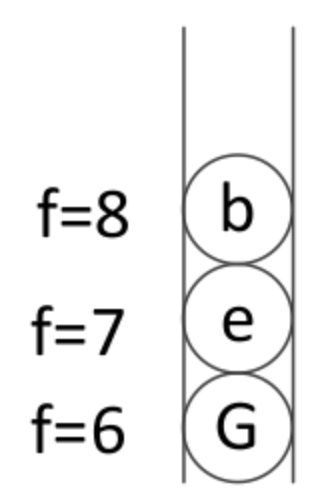
8、弹出f值最小节点
弹出的节点是目标节点G,算法结束
A*算法分析
A_算法的结果是不是最优的?
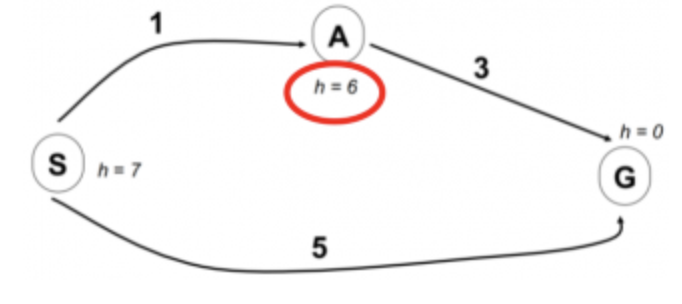
例如这个图,安装A_算法的逻辑找到的路径是 S直接到G ,这样的代价是5。但是经过A节点的代价是4,所以经过A节点的路径是最优的。
问题就是某个节点估计的启发值是不合理的。
如果A_算法想保有最优性,_*需要估计的启发值要小于等于实际的启发值。__
启发函数设计
设计的启发函数为可接受的要满足:需要估计的启发值要小于等于实际的启发值
如果满足上述条件,A_算法的最终结果就是最优的
A_算法使用的时候重点就是如何设计可接受的启发函数
例如用欧式距离作为启发函数,则就是可接受的
用manhattan距离,则就不一定是可接受的
A*应用的更好方式
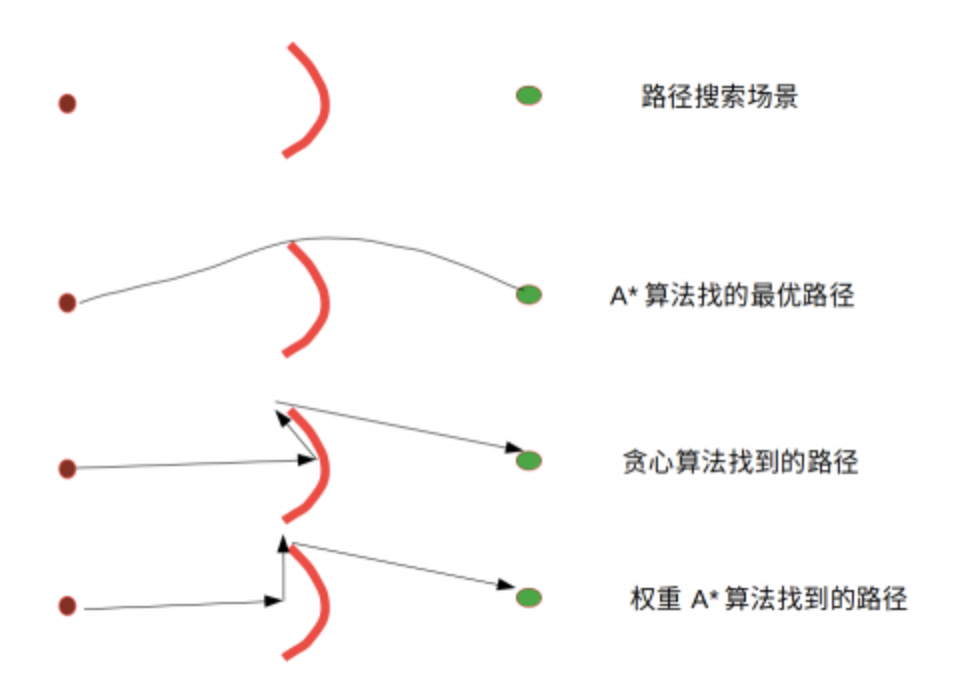
如果我们想用更高的启发估计,相当于A*算法在向贪心算法演变。
相当于虽然不是最优的结果,但是可以带来速度上的提升。
这样的操作就是 权重A_(Weighted A_)
f = g + ah ;a>1 , 越大找到目标的速度越快。
牺牲最优性获取搜索速度
Weighted A* 也有一些升级
例如:
•AntTime A*
•ARA*
•D*
