
一、正则化定义
正则化处理是机器学习和统计模型中常用的一种技术,用于防止模型过拟合(overfitting)。过拟合是指模型在训练数据上表现良好,但在未知数据上表现不佳,模型过于复杂,学习能力太强,把训练数据中的噪声也学习到了,导致泛化能力下降。正则化通过惩罚模型的复杂度来提高模型的泛化能力。
二、正则化(通俗理解)
你是小白,还是感觉有些抽象,看不懂?那你试试这么理解:
过拟合就像是一个学生在考试前死记硬背了很多知识,但是在真正的考试中,遇到一些灵活应用的问题时就不知道怎么解答了。正则化就是让模型不仅学习到训练数据中的特定知识,还能掌握一些更一般化的规律,以便在遇到未知数据时也能做出正确的预测。
可以用一个简单的例子来说明正则化的作用。假设你是一个老师,你要预测学生的数学成绩,你手头有一些数据,比如学生的家庭作业成绩、课堂小测验成绩和期末考试成绩。你可以用这些数据来建立一个模型,但是你担心模型对训练数据过于敏感,不能很好地泛化到新的数据上。
这时,你就可以使用正则化。正则化就像是在你的模型上加上一些限制条件,让模型不要过于关注训练数据中的细节。比如,你可以告诉模型:“我不仅希望你的预测尽可能准确,我还希望你的模型尽可能简单。”这里的“简单”通常意味着模型中的参数不要太多或者太大。
在数学上,正则化通常是通过在模型的损失函数中添加一个惩罚项来实现的。这个惩罚项会根据模型参数的大小来对模型进行惩罚。如果参数太大,惩罚项就会很大,从而使得整个损失函数变大。这样,在优化模型的时候,我们不仅希望减小预测误差,还希望减小参数的大小,从而得到一个更简单的模型。
总的来说,正则化就像是在训练模型时给模型加上一些“规矩”,让模型不要过于依赖训练数据中的特定信息,而能够学习到一些更一般化的规律,从而在遇到未知数据时也能做出准确的预测。
三、正则化方法(类型)
1、L1正则化(Lasso回归):L1正则化通过在损失函数中添加权重向量的绝对值之和的惩罚项来实现。这种正则化方法的一个特点是它能够产生稀疏的模型,即模型中的一些参数会变成0,从而实现特征的自动选择。公式表示为:
J(\theta) = \text{损失函数} + \alpha \sum_{i=1}^{n} |\theta_i|

其中,α 是正则化强度参数,θi 是模型参数。
2、L2正则化(Ridge回归):L2正则化通过在损失函数中添加权重向量的平方之和的惩罚项来实现。L2正则化可以防止模型过拟合,但它不会产生稀疏模型。公式表示为:
J(\theta) = \text{损失函数} + \alpha \sum_{i=1}^{n} \theta_i^2
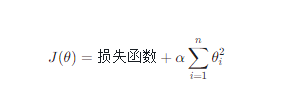
3、Elastic Net:Elastic Net是L1和L2正则化的结合,通过调整混合参数控制L1和L2正则化的比例。这种方法既能够产生稀疏模型,又能够保持L2正则化的优势。
4、Lp正则化:Lp正则化是L1和L2正则化的推广,其中p可以是0到无穷大之间的任意实数。当p=0时,L0正则化会导致模型变得非常稀疏,因为它试图将尽可能多的参数设为0。当p=1时,就是L1正则化;当p=2时,就是L2正则化。
5、Early Stopping:Early Stopping是一种简单的正则化方法,它通过在训练过程中提前停止来防止过拟合。当验证集的错误率开始增加时,训练就会停止。
6、Dropout:Dropout是一种在神经网络中使用的正则化技术,它在训练过程中随机地“丢弃”一些神经元,从而防止过拟合。这种方法迫使网络学习更加鲁棒的特征。
7、数据增强: 数据增强是一种通过增加训练数据的多样性来防止过拟合的方法。在图像识别任务中,可以通过旋转、缩放、裁剪等方式来增加训练样本。
8、集成方法: 集成方法如Bagging和Boosting也可以看作是一种正则化方法,因为它们通过结合多个模型来提高整体的泛化能力。
四、如何选择合适的正则化方法
选择正则化技术时,需要考虑以下因素:
数据特性:如果数据包含大量无关特征,Lasso可能是一个好选择。如果特征之间高度相关,Ridge或Elastic Net可能更合适。
模型复杂性:对于复杂的模型,如深度神经网络,Dropout是一个常用的选择。
计算资源:有些正则化方法,如Dropout,可能会增加计算成本。
调参能力:如果你有足够的资源进行超参数调优,可以选择更复杂的方法,如Elastic Net。如果没有,简单的Early Stopping可能就足够了。
五、正则化如何影响模型复杂度:
参数稀疏化:对于L1正则化(如Lasso),它倾向于产生稀疏的模型,即模型中的许多参数接近于零。这种稀疏性减少了模型的复杂度,因为模型依赖于更少的特征。
参数缩小:对于L2正则化(如Ridge和Elastic Net),它会使模型参数的值减小,但不会产生稀疏模型。这种缩小参数的效果也减少了模型的复杂度,因为它减少了模型对单个特征的敏感性。
降低模型容量:正则化通过限制模型参数的大小,间接地减少了模型的容量。一个高容量的模型可以捕捉到训练数据中的噪声和细节,但可能会在未知数据上表现不佳。正则化帮助模型避免这种情况。
六、正则化参数怎么设置?
经验法:
对于Lasso和Ridge回归,α的值可以从一个非常小的数开始,例如0.001,然后逐渐增加,例如0.01、0.1、1、10等,直到找到一个使模型性能开始下降的值。
对于Elastic Net,除了α值,还需要选择L1正则化与L2正则化的混合比例(如λ),这通常也是从0开始,逐渐增加,例如0.1、0.5、0.9等。
网格搜索:
使用网格搜索(Grid Search)方法,可以定义一个α值的网格,例如从0.001到100,以对数刻度分隔(0.001, 0.01, 0.1, 1, 10, 100)。
网格搜索会在所有可能的α值组合上训练模型,并评估每个组合的性能,但这可能会非常耗时,尤其是当数据集较大或模型复杂时。
随机搜索:
随机搜索(Random Search)是另一种超参数优化方法,它随机选择α值进行尝试,而不是遍历所有可能的组合。
这种方法可以在更短的时间内找到较好的α值,尤其是在参数空间较大时。
交叉验证:
使用交叉验证来评估不同α值下的模型性能。例如,可以设置一个较宽的α值范围,并通过交叉验证来确定哪个α值在验证集上表现最佳。
贝叶斯优化:
贝叶斯优化是一种基于概率的方法,它通过先前的评估结果来指导下一次的参数选择,从而更有效地找到最佳α值。
在选择α值时,重要的是要考虑到正则化的目的是为了防止过拟合,并且要在模型性能和模型复杂性之间找到平衡。通常,最佳的正则化参数会在验证集上给出最好的泛化性能。因此,选择α值的过程应该结合交叉验证,以确保模型在未知数据上也能表现良好。
最后,需要注意的是,正则化参数的选择是一个实验性的过程,可能需要根据具体问题进行调整。在实际应用中,可能需要尝试多种方法和技术,以找到最适合当前数据集和模型的正则化参数。
