
线性规划概述
线性规划(Linear Programming, LP)是运筹学中的一个重要分支,用于在一组线性不等式的约束条件下,找到线性目标函数的最大值或最小值。自1947年G.B. Dantzig提出求解线性规划的单纯形法以来,线性规划在理论和实践中都取得了长足的发展,并广泛应用于经济学、商业、工程等多个领域。
线性规划的基本概念
线性规划问题通常由三个要素构成:决策变量、目标函数和约束条件。决策变量是决策者为了达到预定目标而要控制的量;目标函数是需要优化(最大化或最小化)的线性函数;约束条件则是问题中的线性不等式或等式,用于限制决策变量的取值范围。
线性规划问题可以表示为以下形式:
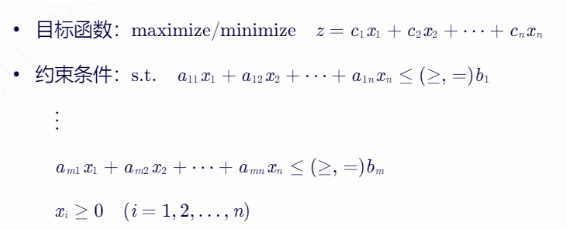
求解方法
线性规划问题可以通过多种方法求解,包括图形方法、单纯形法、对偶单纯形法、内点法等。
图形方法:适用于两个变量的线性规划问题,通过图形直观地找到最优解。
单纯形法:一种迭代算法,适用于大规模问题,通过逐步改变基可行解来寻找最优解。
对偶单纯形法:单纯形法的变体,用于求解原问题的对偶问题,有时可以更高效地找到原问题的解。
内点法:一种基于优化问题内部点的算法,通常用于大规模问题,收敛速度快但可能需要更复杂的数学处理。
线性规划与机器学习的关系
尽管线性规划本身是一种优化方法,但它在机器学习中也扮演着重要角色。机器学习的核心在于从数据中学习并做出预测或决策,而线性规划则提供了一种在给定约束条件下优化目标函数的工具。
线性模型:线性规划的思想在线性模型中得到了直接应用。线性模型(如线性回归、逻辑回归)假设输入和输出之间存在线性关系,其目标函数和约束条件都是线性的。通过最小化目标函数(如均方误差、交叉熵损失等),线性模型可以找到最佳的参数,使得模型预测的结果与实际数据之间的误差最小。
优化问题:在机器学习中,许多算法都涉及到优化问题,如支持向量机(SVM)的求解过程可以看作是一个线性规划问题。SVM的目标是找到一个分类超平面,使得不同类别之间的间隔最大化。通过求解线性规划问题,可以找到满足这一条件的最佳分类超平面。
资源分配与决策支持:在机器学习的实际应用中,线性规划可以用于资源分配和决策支持。例如,在推荐系统中,可以根据用户的偏好和物品的特性,利用线性规划来优化推荐策略,提高推荐效果;在供应链管理中,可以利用线性规划来优化库存水平、生产计划和物流,降低成本并提高效率。
线性规划的应用场景
线性规划的应用场景非常广泛,几乎涵盖了所有需要在多个约束条件下进行优化决策的领域。以下是一些具体的应用实例:
生产计划:企业可以利用线性规划来确定不同产品的生产量,以满足市场需求同时最大化利润。
资源分配:在有限的资源下,如何分配资源以完成多个项目或任务,例如资金、人力或原材料的分配。
投资组合优化:在金融领域,线性规划可以帮助投资者在风险和回报之间找到平衡,构建最优的投资组合。
设施选址:确定新工厂或仓库的最佳位置,考虑到成本、运输、市场需求等因素。
农业规划:在农业生产中,决定不同作物的种植面积,以最大化收益或满足特定的生产目标。
