
矩阵,简而言之,是一个按照长方阵列排列的复数或实数集合。然而,这简单的定义背后隐藏着惊人的力量——它能够将复杂的几何变换以一种简洁而统一的方式表示出来。无论是平移、旋转、缩放还是更复杂的仿射变换,甚至是投影和透视变换,矩阵都能以数学语言精准描述,使得这些变换在计算机中得以高效实现。
一、二维矩阵与平面几何的邂逅
1.1 旋转矩阵:圆舞曲的指挥棒
在二维平面上,旋转是最直观也最具代表性的几何变换之一。通过旋转矩阵,我们可以轻松实现点或图形的旋转。设某点(x, y)绕原点顺时针旋转θ角度后的新坐标为(x', y'),则旋转矩阵为:
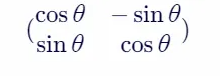
将点(x, y)表示为列向量,与旋转矩阵相乘即得到旋转后的坐标:
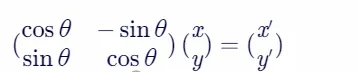
1.2 缩放矩阵:大小的魔术师
缩放变换同样简单直接,通过改变坐标轴上的比例因子来实现。沿x轴和y轴分别缩放kx和ky倍的缩放矩阵为:
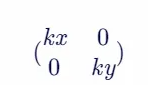
与点(x, y)的列向量相乘,即可得到缩放后的坐标。缩放矩阵就像是掌握着物体大小的魔术师,轻轻一挥,便能让图形在尺寸上随心所欲地变化。
1.3 平移矩阵:位置的搬运工
值得注意的是,在标准的二维线性变换中,平移并不直接由矩阵乘法实现(因为平移不是线性变换),但可以通过引入齐次坐标(即在二维坐标后添加一个恒为1的维度)来构造平移矩阵。平移矩阵形如:
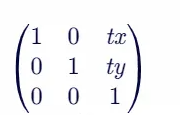
这里,tx和ty分别是沿x轴和y轴的平移量。通过齐次坐标,平移变换也得以融入矩阵变换的大家庭,成为几何变换的得力助手。
二、三维矩阵与立体世界的对话
当矩阵的维度扩展至三维时,其几何意义变得更加丰富和复杂。三维空间中的点(x, y, z)通过三维矩阵可以实现旋转、缩放、平移乃至更复杂的变换,如斜切、镜像等。
2.1 旋转矩阵的多样性
在三维空间中,旋转可以围绕任意轴进行,这使得旋转矩阵的构造变得复杂。常见的做法是先通过一系列基本旋转(如绕x轴、y轴或z轴旋转)的复合来实现任意轴的旋转。每个基本旋转都可以用一个3x3的矩阵表示,而复合旋转则是这些矩阵的乘积。
2.2 仿射变换与投影变换
仿射变换是线性变换与平移的组合,它在三维图形学中尤为重要,用于实现视角变换、物体定位等。而投影变换则更进一步,它模拟了光线通过特定角度照射到物体上并在平面上形成影像的过程,是计算机图形渲染的基础。投影矩阵能够将三维空间中的点映射到二维屏幕上,是实现3D到2D转换的关键。
三、矩阵计算的几何直观性
矩阵计算之所以在几何变换中如此重要,很大程度上归功于其直观性。通过矩阵,我们可以将复杂的几何变换分解为一系列简单的线性操作(如旋转、缩放)和非线性操作(如平移,通过齐次坐标实现),这些操作可以像搭积木一样组合起来,形成任意复杂的变换。这种模块化和组合性的特性,不仅简化了变换的表示,也极大地提高了变换的计算效率和可重用性。
四、矩阵计算的深层几何意义
4.1 变换的连续性与平滑性
矩阵计算不仅限于静态的几何变换,它还能描述变换的连续性和平滑性。通过参数化矩阵中的元素,我们可以创建随时间变化的变换序列,如动画中的物体运动轨迹。这种连续性和平滑性在动画、游戏开发、虚拟现实等领域至关重要,它使得虚拟世界中的物体运动更加自然和逼真。
4.2 坐标系的转换
矩阵还可以用于坐标系的转换。在不同的应用场景中,我们可能需要从一个坐标系转换到另一个坐标系来观察或计算物体。例如,在机器人学中,机器人手臂的末端执行器需要在不同的参考坐标系下进行定位和定向。通过构建适当的变换矩阵,我们可以轻松实现不同坐标系之间的转换,从而简化问题的求解过程。
4.3 线性空间的映射
从更抽象的角度来看,矩阵计算实际上是在进行线性空间之间的映射。线性空间是数学中的一个基本概念,它包含了一系列的向量以及这些向量之间的线性运算。矩阵可以看作是从一个线性空间到另一个线性空间的线性映射的表示。通过矩阵的乘法运算,我们可以将一个线性空间中的向量映射到另一个线性空间中的新向量,这种映射保持了向量的线性关系不变。
五、矩阵计算在实际应用中的几何光芒
5.1 计算机图形学
计算机图形学是矩阵计算几何意义最直观的体现之一。在图形渲染过程中,无论是模型的变换、视图的设置还是光照的计算,都离不开矩阵的参与。通过矩阵,我们可以轻松实现物体的旋转、缩放、平移以及摄像机视角的调整等变换操作,从而生成逼真的三维图像和动画效果。
5.2 机器人学
在机器人学中,矩阵计算被广泛应用于机器人的运动规划和控制中。机器人手臂的运动可以看作是一系列关节角度的变化过程,这些变化可以通过矩阵变换来描述和计算。通过构建机器人手臂的正运动学模型(即关节角度到末端执行器位置的映射),我们可以利用矩阵计算来求解机器人手臂在给定关节角度下的末端执行器位置;反之,通过逆运动学计算,我们可以求解出达到特定末端执行器位置所需的关节角度。
5.3 工程学
在工程领域,矩阵计算同样发挥着重要作用。例如,在结构力学中,我们可以通过建立结构的刚度矩阵和质量矩阵来求解结构的动力响应问题;在控制理论中,状态空间表示法利用矩阵来描述系统的动态特性,并通过矩阵运算来设计控制器以实现系统的稳定控制。
